|
Кузнецов Л.А. Дифференциальные уравнения. Задача 11
Уравнения вида 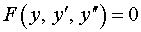
Постановка задачи. Найти решение задачи Коши для дифференциального уравнения
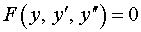
с начальными условиями 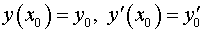 . .
План решения.
1. Поскольку дифференциальное уравнение не содержит явно независимой переменной 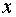 , полагаем , полагаем
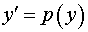 , ,
где 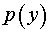 – новая неизвестная функция. Тогда по формуле для производной сложной функции имеем – новая неизвестная функция. Тогда по формуле для производной сложной функции имеем
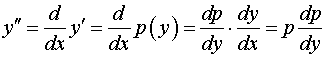 . .
Получили уравнение первого порядка относительно 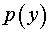
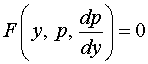 . .
2. Определяя тип этого уравнения и применяя соответствующий метод решения, находим 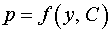 , где , где 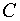 – произвольная постоянная. – произвольная постоянная.
3. Используя начальные условия, находим 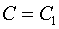 . .
4. Подставляя 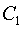 , получаем дифференциальное уравнение с разделяющимися переменными , получаем дифференциальное уравнение с разделяющимися переменными
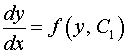 . .
Разделяя переменные в области, где 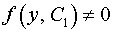 , получаем , получаем
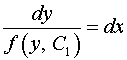
и, интегрируя, находим 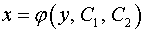 . .
Проверяем, не является ли решение 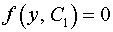 особым решением исходного уравнения, удовлетворяющим начальным условиям. особым решением исходного уравнения, удовлетворяющим начальным условиям.
5. Используем начальные условия для нахождения второй постоянной 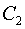 и получаем решение задачи Коши. и получаем решение задачи Коши.
Задача 11. Найти решение задачи Коши.
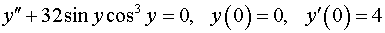 . .
Замена 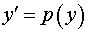 , откуда , откуда 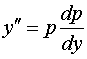 . .
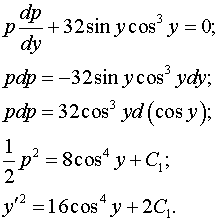 . .
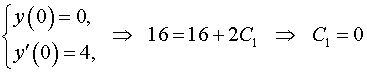
Получаем
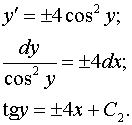 . .
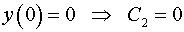
Решение задачи Коши:
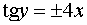
или
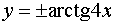 . .
Купить решение своего варианта с оплатой по SMS
:: Рекомендуемая литература.
Ремендуем покупать учебную литературу в интернет-магазине
VIP Казань — Казань для достойных людей
|

