|
Кузнецов Л.А. Интегралы. Задача 12
Интегрирование выражений  и и 
Постановка задачи. Найти неопределенные интегралы вида:
а)  ; ;
б)  ; ;
в)  ; ;
где 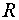 – рациональная функция. – рациональная функция.
План решения.
1. Чтобы избавиться от радикала, используем тригонометрические или гиперболические подстановки:
а)  или или  ; ;
б)  или или 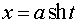 ; ;
в)  или или  . .
2. Применив формулу замены переменной, получим интегралы вида
 . .
3. Вычисляем последний интеграл с помощью известных подстановок или методом понижения степени.
4. Возвращаемся к переменной  и записываем ответ. и записываем ответ.
Замечание. В случае определенного интеграла все аналогично, только необходимо изменить пределы интегрирования соответствующим образом.
Задача 12. Вычислить определенные интегралы.

Купить решение своего варианта с оплатой по SMS
:: Рекомендуемая литература.
Ремендуем покупать учебную литературу в интернет-магазине
VIP Казань — Казань для достойных людей
|

